The checksum is used for data transfer or storage in the digital environment, for error detection and data integrity. In order to be able to detect file integrity, it is necessary to add an extra element to the initial data. Control is done via this extra added element.
A checksum is generated from a data input given as a function or algorithm. A good checksum algorithm is one that produces a totally different set of checksums even with minimal changes on the input.
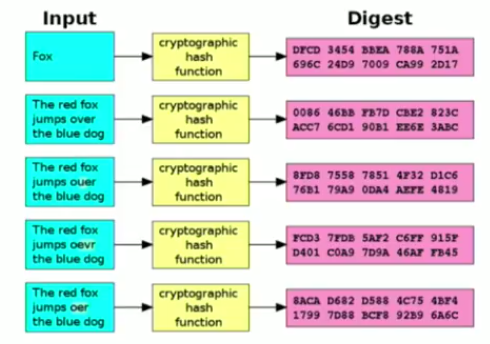Effect of Sha-1 algorithm on different inputsAs shown in the figure, Sha-1 algorithm gives a completely different result even when the slightest change is made on two very similar inputs.
If the pre-calculated checksum and the checksum calculated after the data entry are equalized, it can be assumed that the data is not corrupted or changed accidentally by a very high probability.
Basic Algorithms
The simplest checksum algorithm is considered as longitudinal redundancy check. The process is simple: Divide the data by a fixed number of bits, then calculate the XOR values of all the bits of these parts separately. The result of this computation (checksum) is appended to the end of the data entry. The integrity of the data entry is provided as a result of calculating the XOR values of the receiver, including the checksum of all fragments. If the result obtained by the receiver is not a piece of zeros, it is understood that an error has occurred during the transmission.
Set LRC = 0
For each byte b in the buffer
do
LRC = LRC XOR bThis checksum algorithm will not encounter a problem unless the bits that have changed during transmission are in odd numbers.
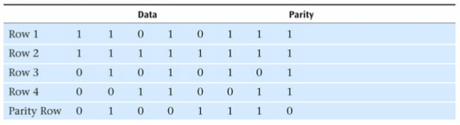A simple example of longitudinal redundancy checkHowever, if there are even number of errors and these errors are in the same position in two separate parts, the algorithm will not be able to detect any errors. When there are a number of different bits, the probability that the algorithm can not find an error is calculated as 1/n.
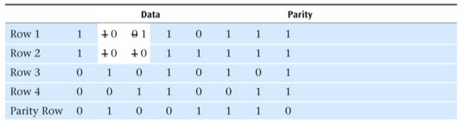An example of an error that can not be detected by longitudinal redundancy checkAnother form of longitudinal redundancy check algorithm is the modular one. In this version all the parts of the data to be sent are converted into byte values and summed.
22 67 21 51 25 12It is then divided into the designated value (defined by algorithm to use in receiver and the transmitter) for use in the calculation. The remainder from this calculation is the checksum value.
198 % 64 = 6The checksum we calculated, is appended to the end of the data to be transmitted.
22 67 21 51 25 12 6The party that receives the data assumes that there is no data loss or change during the transfer if the same calculations (without adding checksum) result in the same checksum value.
However, as in the previous variant, there are some deficits in this algorithm. Even though the algorithm does not encounter a problem detecting the difference when there is inconsistency in the value of only one part,
21 67 21 51 25 12If there are two differences that close the gap between each other, the algorithm will have problems not detecting the difference.
21 68 21 51 25 12More commonly used checksum algorithms, such as Adler-32, Fletcher's checksum address the problems of the above mentioned algorithms, by considering the positions of bits as well. However will also increase resource allocation in checksum generation and checking for many situations.